马尔可夫模型
9.3 隐马尔可夫模型的三个基本问题
- 给出一个模型$\mu=(A,B,\pi)$,怎样有效地计算某个观测序列发生的概率,即$P(O|\mu)$?
- 给出观测序列$O$和模型$\mu$,我们怎样选择一个状态序列$(X_{1},...,X_{T+1})$,以便能够最好地解释观测序列?
- 给定观测序列$O$,以及通过改变模型$\mu=(A,B,\pi)$的参数而得到的模型空间,我们怎样才能找到一个最好地解释这个观测序列的模型。
这中间包含了三个量:
- 观测序列$O$
- 模型$\mu$
- 状态序列$(X_{1},...,X_{T+1})$
第一个是马尔可夫模型的正向用途,第二个是求出隐藏状态,第三个则是学习过程,即通过现象去学习一个模型。
9.3.1计算观测序列的概率
每个状态到达观测序列$O$都有一定的概率,我们将所有状态到达观测状体的概率相加不就可以得到在给定模型$\mu$的情况下,观测序列$O$出现的概率。
给定一个状态序列$(X_{1},...,X_{T+1})$,然后对应的到达$O$的概率就为
$$P(O|X,\mu)=\Pi_{t=1}^{T}P(O_t|X_t,X_t+1,\mu) =b_{X_{1}X_{2}o_{1}} b_{X_{2}X_{3}o_{2}}...b_{X_{T}X_{T+1}o_{T}}$$
出现这个状态序列的概率为
$P(X|\mu)=\pi_{x_1}a_{X_1 X_2}a_{X_2 X_3}...a_{X_TX_{T+1}}$
因此
$P(O,X|\mu)=P(O|X,\mu)P(X|\mu)$
最终
$P(O|\mu)=\sum_X P(O|X,\mu)P(X|\mu)$
分析一下这个算法,虽然说这个算法非常直观,推导也是初学者级别(没错就是我),但是首先给定一个$X$我们想要算出$P(O,X|\mu)=P(O|X,\mu)P(X|\mu)$就需要$T-1+T+1$次的乘法,然后$X$还有$N^{T+1}$个组合,算出每个组合就需要$(2T)N^{T+1}$次乘法,再将这些组合的结果相乘,就得到了$(2T+1)N^{T+1}$次乘法的需求。
直觉告诉我这里面有重复计算的结果,其实整个计算过程和动态规划很像,每条边都有代价
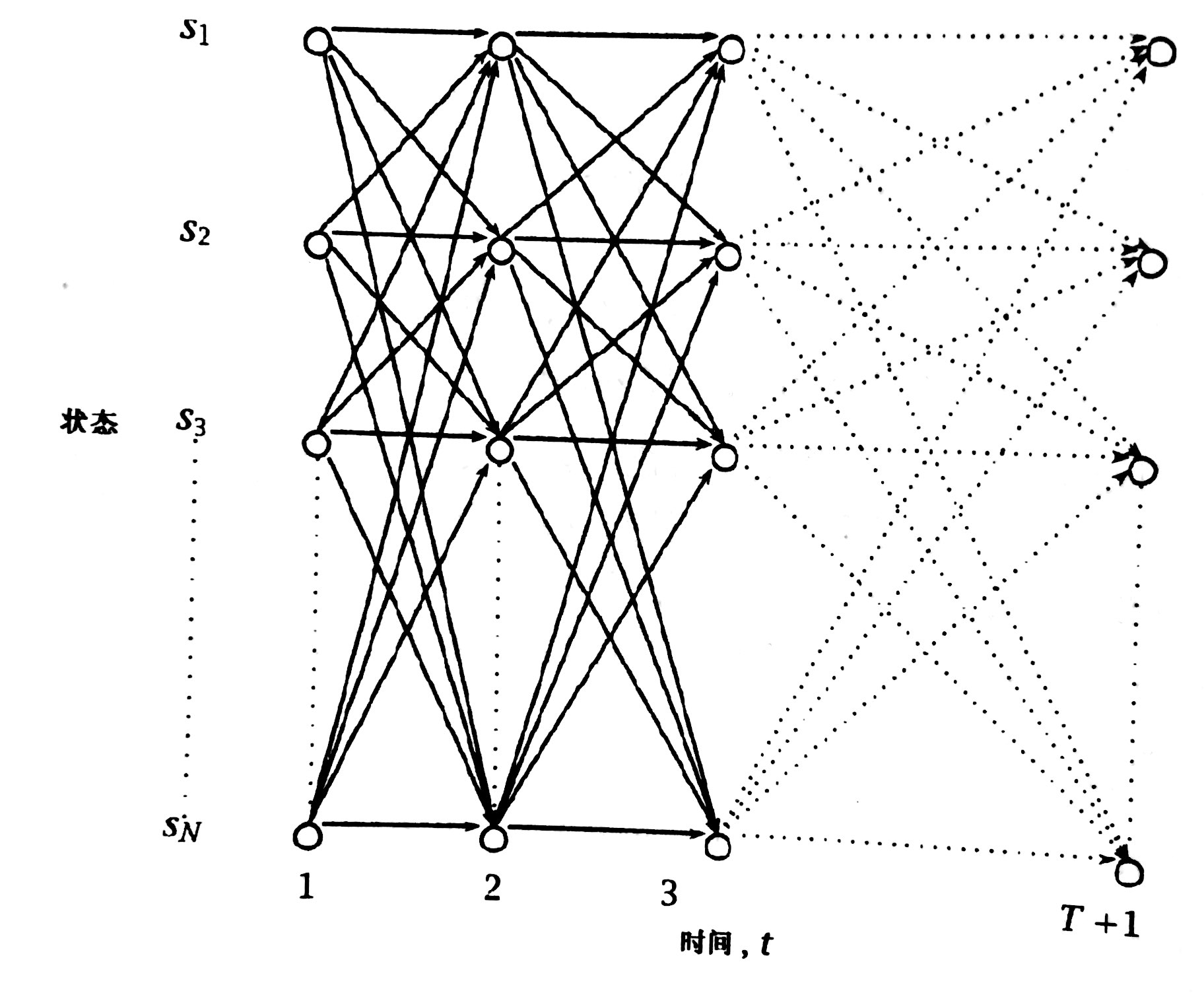
一个格子$(S_i,t)$存储了一些信息。
前向过程
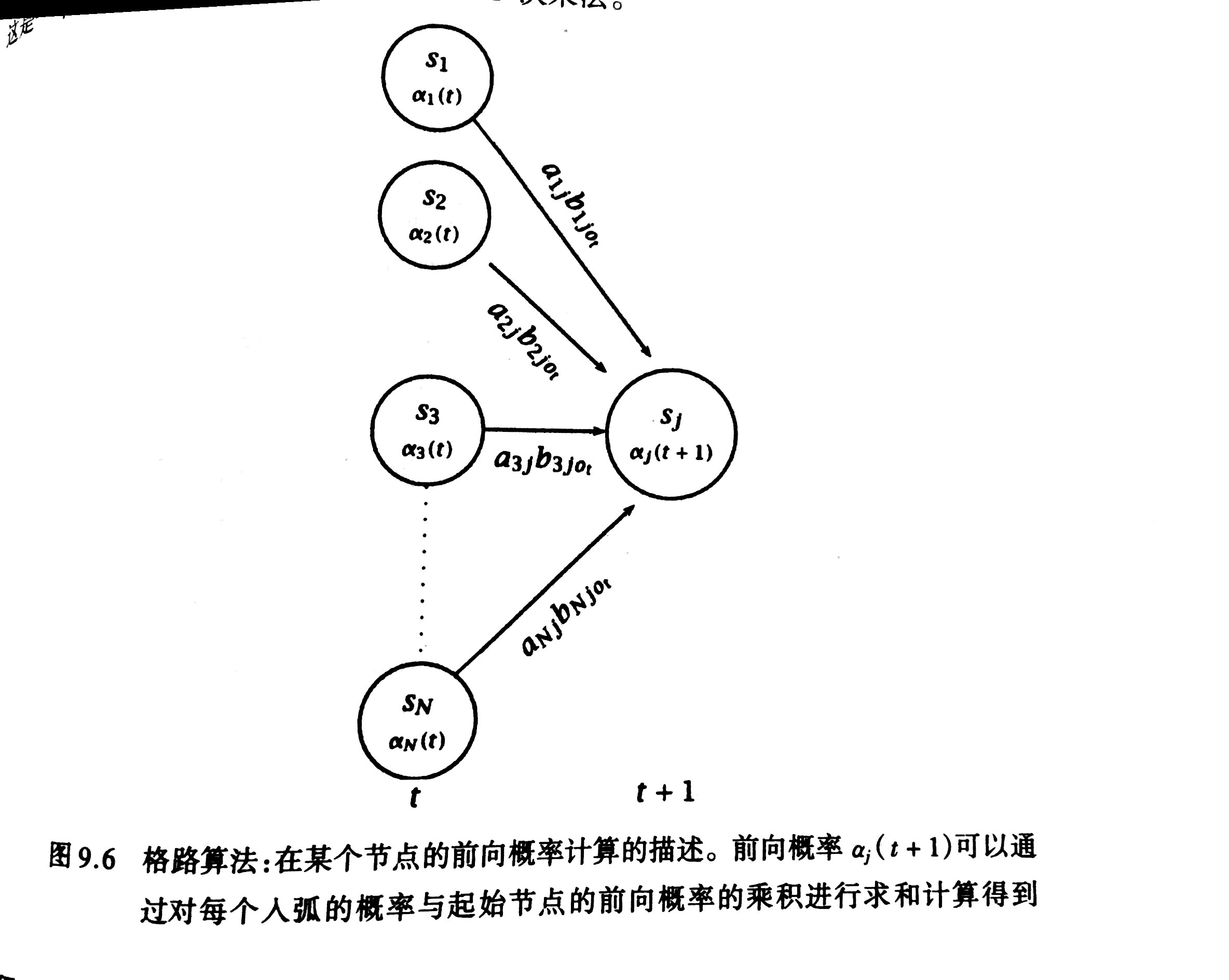
$\alpha_i(t)=P(o_1 o_2 ... o_{t-1},X_t=i|\mu)$
$\alpha_i(t)$存储在格路的$(S_i,t)$中,表示在$t$时刻已状态$S_i$结束的概率。
- 初始化
$\alpha_i(1)=\pi_i,1 \leq i \leq N$
- 推导
$\alpha_i(t+1)=\sum_{t=1}^{N} \alpha_i(t) a_{ij}b_{ijo_t},1\leq t\leq T,1\leq j\leq N$
- 求和
$P(O|\mu)=\sum_{i=1}^N\alpha_i(T+1)$
用前向过程来计算观测序列的概率,可以只需要$2N^2T$次乘法就可以搞定了。
后向过程
这个过程是和前向相对应的,所表示的意思是从当前t时刻开始,观测到$T$这样的观测序列,并且知道t时刻的隐藏状态是$X_{t}$。在给定的模型$\mu$的情况下,能观察到之前的序列的概率就称为后向过程。之所以要引入后向概率是为了解决三个基本问题中的第三个问题。
给出的公式如下:
$\beta _{i}(t)=P(o_{t}...o_{T},X_{t},\mu)$
后向过程理解起来会有点难度,特别是像我这样直观先行的动物来说,对于公式总得翻译得直白一点才能想想。这个过程也就是当某一时刻$X_t=i$的情况下,开始转换的到最后能得出$o_{t}...o_{T}$这个观测序列的概率,也就是$\beta _{i}(t)$,这样我们可以依赖于。如果我们知道$\beta _{i}(t+1)$的值的话,这个就很简单了,$\beta _{i}(t)$想要到达最后的概率是通过各个$\beta _{i}(t+1),1 \leq i \leq N$的节点到达最后的概率只喝,因此它的推导公式就很好理解了。
- 初始化
$\beta _{i}(T +1)=1, 1\leq i\leq N$
- 推导
$\beta _{i}(t)=\sum_{j+1}^{N}a_{ij}b_{ijo_t}\beta _{j}(t+1),1\leq t\leq T 1\leq i \leq N$
- 求和
$P(O|\mu)=\sum_{i=1}^{N}\pi_i\beta_i(1)$
前向后向的结合
我们可以让前向后向公式结合来计算一个观测序列的概率
$P(O,X_{t}=i|\mu)=\alpha_{i}(t)\beta_{i}(t)$
有了这个中间公式之后,我们就可以计算
$P(O|\mu)=\sum_{i=1}^{N}\alpha_{i}(t)\beta_{i}(t),1\leq t \leq T +1$
到此为止,我们解决了第一个问题了
9.3.2确定最佳状态序列
这个过程通常被称为是一个译码,被人模糊地描述为“找到能够最好地解释观测值的状态序列”。存在两种方法:
对于每一个$t,1\leq t \leq T+1$,我们可以找到$X_t$,使得$P(X_t|O,\mu)$最大
但这个方式实际上是最大化了奖杯正确猜测的状态的期望数目,所以最常用的方法是
Viterbi算法。
Viterbi算法
我们希望找到一个状体序列$X$:
$\arg\max_{X} P(X|O,\mu)$
我们可以比较容易得到在一个模型$\mu$下,同时得到一个观测序列$O$和状态序列$X$的概率是多少,固定观测序列后,前面的问题的解等价于下面这个问题的解。
$\arg\max_{X} P(X,O|\mu)$
这个地方我需要解释一下,这个问题是如何转移的
$P(X,O|\mu)=P(X|O,\mu)P(O|\mu)$
然后由于$P(O|\mu)=1$,因为它是给定的,所以概率当然为1啦。因此左右两边相等,因此前面的问题等价可以成立。
为了解决这个问题,定义:
$\delta_j(t)=\max_{X_1...X_{t-1}} P(X_1 ... X_{t-1},o_1 ... o_{t-1},X_t=j|\mu)$
变量$\psi_j(t)$记录了导致这条最可能路径的入弧节点。还是用动态规划的思想来解决。
初始化
$\delta_j(t)=\pi_j,1 \leq j \leq N$
推导
$\delta_j(t+1)=\max_{1 \leq i \leq N}\delta_i(t)a_{ij}b_{ijo_t},1\leq j\leq N$
然后存储回溯路径
$\psi_j(t+1)=\arg\max_{1 \leq i \leq N}\delta_i(t)a_{ij}b_{ijo_t},1\leq j\leq N$
终止以及路径读出
$$\hat{X}_{T+1}=\arg\max_{1 \leq i \leq N}\delta_i(T+1)\\ \hat{X}_t=\psi_{\hat{X}_{T+1}}(t+1)\\ P(\hat{X})=\max_{1 \leq i \leq N}\delta_i(T+1)$$
9.3.3隐马尔可夫的参数估计问题
这个问题可以看作是求解下面这个式子。这个已经可以算是机器学习的问题,对一个式子进行最优化,这里用的最优化方法是EM算法的一个特例。因为这个问题没有一个解析解,并不像之前的两个问题一样。这个方法叫做迭代爬山算法,也叫做Baum-Welch或前向后向算法。
$\arg \max_{\mu} P(O_{training}|\mu)$
过程
$p_t(i,j)$是在给定观测序列$O$的情况下,在$t$时刻经过某条弧的概率。$$p_t(i,j)=P(X_t=i,X_{t+1}=j|O,\mu)\\ =\frac{P(X_t=i,X_{t+1}=j,O|\mu)}{P(O|\mu)}\\ =\frac{\alpha_i(t) a_{ij}b_{ijo_t} |beta_j(t+1)}{\sum_{m=1}^N\alpha_m(t)\beta_m(t)}\\ =\frac{\alpha_i(t) a_{ij}b_{ijo_t} |beta_j(t+1)}{\sum_{m=1}^N \sum_{n=1}^N \alpha_m(t) a_{mn}b_{mno_t}\beta_n^{t+1}}$$
求解上面这个式子是这个问题的关键,因为更新$\pi$,$A$和$B$都需要这个式子
计算这个的时候需要先计算出前向过程和后向过程,上面这个式子实际上可能是有误导性的,因为虽然它把这个分的这么细,但实际上都需要前向和后向过程,所以可以直接获得$P(O|\mu)$。然后分子就更好算了,其中四个量都是已知的。有了$p_t(i,j)$之后,$a_{ij}$就是可以更新为所有从i出发到达j的弧的概率除以从i出发的概率,$\pi_i$则是在$t=1$时刻的从$i$出发的弧的个数除以$t=1$时刻出发的所有弧的个数。$b_{ijk}$则是所有从i到j的弧中,发射出状态k的概率。
这样之后一次参数更新就完成了,我们就有了新的模型,当观察序列的出现概率没有显著增长的话,算法就可以停止了。